Characteristics of Design and Statistical Analysis of NEI-funded Ophthalmic Clinical Trials
Abstract
Objective:
To describe the characteristics of trial design and statistical analysis of the National Eye Institute (NEI)-funded randomized clinical trials (RCTs) conducted after the year 2000.
Design:
Review of 42 NEI-funded ophthalmic RCTs.
Methods:
Eligible trials were identified from ClinicalTrials.Gov and their primary result papers were identified from PubMed. Data on the design characteristics (primary outcome, number of arms, sample size, statistical power, inclusion of one eye or two eyes) and statistical analysis (statistical method for adjustment of inter-eye correlation, correction for multiple comparisons) as reported in the primary result paper were collected independently by two authors, and the differences were adjudicated by the senior author. Descriptive analyses were performed to summarize the characteristics of trial design and statistical analysis.
Main Outcome Measures:
Characteristics of trial design and statistical analysis.
Results:
Forty-two NEI-funded ophthalmic trials conducted after 2000 were included. The majority of trials were for evaluating the efficacy of drugs (57%), medical devices (21%), or procedures (14%) for the treatment of retinal diseases (45%) or pediatric eye diseases (45%). All trials were designed with at least 80% statistical power for comparing continuous (64%), binary (24%), or time-to-event (12%) primary outcome measures. In 11 (26%) trials enrolling both eyes of a participant, two eyes were in the same treatment group in 6 (55%) trials, and two-eye data were properly analyzed with adjustment for the inter-eye correlation when needed for all these trials. However, none of these trial publications explicitly stated that the inter-eye correlation was considered in the sample size and power calculation. In 13 trials with more than two arms, 12 (92%) trials adjusted for multiplicity using Bonferroni correction (42%), Hochberg procedure (42%) or Turkey’s method (17%).
Conclusion:
While the availability of two eyes of a participant may complicate the ophthalmic trial design and statistical analysis, NEI-funded trials followed good practice in the trial design and statistical analysis, with enrollment of two eyes of a participant when appropriate, and adjustment of the inter-eye correlation in the statistical analysis. The sample size and power calculation can be improved by considering the inter-eye correlation and clearly reporting such information for future ophthalmic trials is important.
1. INTRODUCTION
A randomized clinical trial is the gold standard for evaluating the efficacy and safety of treatment for eye diseases. Because each subject has two eyes, and many eye diseases (e.g., significant refractive error, dry eye, glaucoma, retinal diseases) can be present in both eyes at same time, ophthalmic trials have some unique features in the trial design and statistical analysis depending on whether two eyes of a participant are enrolled into a trial (e.g., one eye design vs. two-eye design) [1], and whether the two eyes are assigned to the same treatment group or different treatment groups [2-9]. Additionally, since outcome measures from two eyes of the same subject tend to be positively correlated, the appropriate trial design and statistical analysis need to account for their inter-eye correlations [10].
Lee et al. reviewed 69 ophthalmic clinical trial papers published in 4 major clinical ophthalmology journals (Ophthalmology, JAMA Ophthalmology, American Journal of Ophthalmology, and British Journal of Ophthalmology) in 2009, and found substantial heterogeneity in the quality of the trial design and statistical analysis [1]. In particular, they found that among 13 trials with two-eye design, only 5 (38%) trials used the proper statistical methods for adjusting for the inter-eye correlation, and none of them explicitly stated the adjustment of the inter-eye correlation in the sample size and power calculation. In a recent review of 96 ophthalmic clinical trial papers published in these same 4 ophthalmology journals in 2021, Dong et al. found that in 31 trials with two-eye design, only 13 (42%) trials properly adjusted for the inter-eye correlation in the statistical analysis [9].
The clinical trials funded by the National Eye Institute (NEI) went through comprehensive scientific review by biostatisticians, and clinical trialists for trial design and statistical analysis plan before their approval for funding, and the funded trials were led by a team of investigators with experience in conducting ophthalmic trials. It is reasonable to assume that the NEI-funded trials had fewer flaws in the trial design and statistical analysis. Thus, we conducted a review of NEI-funded trials to evaluate their quality in terms of the study design and statistical analysis. This paper reports our findings on the characteristics of design and statistical analysis of NEI-Funded late phase randomized ophthalmic clinical trials conducted after 2000.
2. METHODS
On June 1, 2022, we searched for phase 2/3 or phase 3 randomized ophthalmic clinical trials from ClinicalTrials.Gov that were funded by the NEI and started the trial after the year 2000 with the primary result paper (e.g., paper reporting the trial primary outcome results) published by June 1, 2022. In ClinicalTrials.Gov, we searched with the following keywords: “eye diseases” in the condition/disease box, “Phase 3” for phase, “NIH” for funding type, and study start date: “01/01/2000”.
For each trial identified from the search in ClinicalTrials.Gov, two authors (WZ, RZ) independently searched for the primary result paper using the following approaches:
1. PubMed search using NCT number or title of the clinical trial and/or PI name
2. ClinicalTrials.Gov list of publications
3. Google searching using the NCT number or title of the clinical trial and/or PI name
If a primary result paper could not be found from the above search approaches, the trial was not included in this review.
From the primary result paper of each eligible trial, we collected data on the trial design characteristic including the phase of the trial, type of eye disease, type of intervention (drug, medical device, treatment procedure etc.), type of design (one-eye design, two-eye design), number of arms, sample size, statistical power, number of clinical sites, the data type of primary outcome (continuous, categorical, time-to-event), sidedness of statistical test (one-sided or two-sided), type of comparisons (non-inferiority, superiority, equivalence), correction for multiple comparisons, statistical tests for comparison of the primary outcome. In addition, for the trial with two-eye design, we collected information on whether two eyes were in the same or different treatment groups, whether the inter-eye correlation was adjusted for in the trial design and statistical analysis, and the statistical method applied for adjusting for the inter-eye correlation.
All these data extractions were independently performed by two authors (WZ, RZ) and the differences were adjudicated by the senior author (GSY). Descriptive analyses were performed using R to summarize the characteristics of trial design and statistical analysis.
This study was conducted by reviewing published papers; it did not involve any human subjects. Thus, the institutional review board approval and the Declaration of Helsinki do not apply.
3. RESULTS
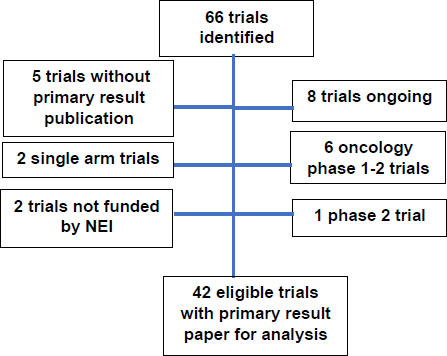
The search in Clinicaltrials.gov found a total of 66 clinical trials (Fig. 1). After excluding 8 ongoing trials that have not yet published primary outcome paper, 6 oncology early phase trials, 5 completed trials yet has not published primary result paper, 2 single-arm trials, 2 trials not funded by NEI, and one phase 2 trial, a total of 42 eligible trials were included in the review for this study.
The characteristics of these 42 eligible trials are reported in Table 1. These 42 trials were mostly funded for evaluating the treatment of retinal diseases (45%) and pediatric eye diseases (45%). The treatment evaluated in these trials was mostly for drugs (57%), medical devices (21%), or treatment procedures (14%).
| Disease Area | n (%) |
|---|---|
| Retina | 19 (45.2%) |
| Pediatric eye disease | 19 (45.2%) |
| Cornea | 2 (4.9%) |
| Oculoplastics | 1 (2.4%) |
| Uveitis | 1 (2.4%) |
| Intervention Type | - |
| Drug | 24 (57.1%) |
| Device | 9 (21.4%) |
| Procedure | 6 (14.3%) |
| Behavioral | 2 (4.8%) |
| Dietary Supplement | 1 (2.4%) |
| Trial Design | - |
| Parallel design | 39 (92.9%) |
| Factorial design | 2 (4.8%) |
| Matched design | 1 (2.4%) |
| Phase | - |
| Phase 2/3 | 4 (9.5%) |
| Phase 3 | 38 (90.5%) |
| Types of Comparison | - |
| Superiority | 35 (83.3%) |
| Noninferiority | 6 (14.3%) |
| Equivalence/noninferiority | 1 (2.4%) |
| Number of Treatment Arms | - |
| 2 | 29 (69.0%) |
| 3 | 7 (16.7%) |
| 4 | 6 (14.3%) |
| Masking | - |
| None | 13 (31.0%) |
| Single | 9 (21.4%) |
| Double | 9 (21.4%) |
| Triple | 3 (7.1%) |
| Quadruple | 8 (19.4%) |
| - | |
| Types of Primary Outcome | - |
| Continuous | 27 (64.3%) |
| Binary | 10 (23.8%) |
| Time-to-event | 5 (11.9%) |
| Sample Size | - |
| Median (Q1, Q3) | 265 (190, 528) |
| Range | 19, 11267 |
| Number of Sites | - |
| Median (Q1, Q3) | 41 (18, 61) |
| Range | 1, 128 |
| Statistical Power of the Trial* | - |
| 80 | 17 (40.5%) |
| 85 | 1 (2.4%) |
| 88 | 1 (2.4%) |
| 89 | 1 (2.4%) |
| 90 | 19 (45.2%) |
| 93 | 1 (4.8%) |
| Side of Statistical Test | - |
| One-sided | 9 (21.4%) |
| Two-sided | 33 (78.6%) |
| - | |
| Multiple Comparisons Corrected for in 13 Multi-arm trial | - |
| No | 1 (7.7%) |
| Yes | 12 (92.3%) |
| Method for Correction of Multiple Comparisons in 12 Trials with Correction | - |
| Bonferroni | 5 (41.7%) |
| Hochberg | 5 (41.7%) |
| Tukey | 2 (16.7%) |
| Both Eyes Included into Trial | - |
| No | 31 (73.8%) |
| Yes | 11 (26.2%) |
| Trial with Statistically Significant difference in Primary Outcome* | - |
| No | 22 (53.7%) |
| Yes | 19 (46.3%) |
In terms of trial design, the majority (n=39, 93%) of trials used the parallel design. These trials included 35 trials (83.3%) for evaluating superiority, 7 (17%) trials for evaluating non-inferiority, and 1 (2%) trial for equivalence. More than two-thirds (69%) of these trials had two comparison arms, and 13 (31%) had three or four arms. Correction for multiple comparisons from multiple arms was performed in 12 (92%) of these 13 multiple-arm trials using the Bonferroni method (42%), Hochberg procedure (42%), or Tukey’s method (17%).
Sample sizes (based on actual enrollment) of these trials ranged from 19 to 11267 with a median of 265 participants (inter-quartile: 190-528). The number of clinical sites for enrolling participants ranged from one to 128 with a median of 41 (inter-quartile: 18 to 61). With the exception of one pilot trial without providing statistical power, all trials were designed with statistical power at least 80%, with 17 trials (41%) having 80% power, 3 (7%) trials having power 85-90%, and 21 trials (51%) having power 90% or above. Thirty-three (80%) trials were designed with two-sided tests.
The primary outcome measure was continuous in 27 (64%) trials, binary in 10 (24%) trials, and time-to-event outcome in 5 (12%) trials. Masking was implemented in 29 (69.0%) trials, including single masking (21%), double masking (21%), triple (7%), or quadruple (19%) masking. In 41 trials with a comparison of primary outcome, a statistically significant difference in primary outcome measure was found in 19 (46%) trials.
3.1. Characteristics of Trials with Two-eye Design
Among the 42 trials, 11 (26%) studies included both eyes in some or all trial participants (Table 2). Among these eleven trials, primary outcome measurement was continuous in 7 trials, binary in 2 trials, and time-to-event in 2 trials. The percentage of participants who contributed both eyes to the trial ranged from 20% to 100% (median 65%). Two eyes of a participant were either assigned to the same treatment group (n=6, 55%) or different treatment groups (n=5, 45%).
Among these 11 trials, the primary outcome was measured at eye level in 9 trials. None of these trials explicitly stated in the primary result publication that the inter-eye correlation was accounted for in the sample size and power calculation. For statistical analysis, 8 of these 9 trials with eye-level outcomes were analyzed at eye-level, and a proper statistical analysis method was applied to account for the inter-eye correlation. In one trial, the average of spherical equivalent from two eyes was used for the comparison of treatment effect because of the high inter-eye correlation in spherical equivalent.
| Trial Number | Number of Subjects/Eyes | Primary Outcome | Data Type of Primary Outcome | Two Eyes in the Same Treatment Group? | Statistical Analysis Accounted for Inter-eye Correlation | Statistical Method to Adjust for Inter-eye Correlation | Other Methods could be Used |
|---|---|---|---|---|---|---|---|
| NCT00027222 (ETROP) | 401 subjects 718 eyes (79% bilateral) |
Unfavorable grating acuity outcomes at 9 months | Binary | No | Yes | Modified Mantel-Haenszel chi-square test | GEE |
| NCT00346333 | 225 subjects 382 eyes (70% bilateral) |
Central visual field score | Continuous | Yes | Yes | Mixed-effects model clustered Wilcoxon test | GEE |
| NCT00542178 (ACCORD Eye study) | 3537 subjects 7074 eyes (100% bilateral) |
3 or more steps of progression on the ETDRS person scale or treatment of retinopathy with photocoagulation or vitrectomy | Binary | Yes | No need to adjust because the ETDRS scale was defined at the person level | Ordinary logistic regression model | GEE if the outcome is defined at eye-level |
| NCT00367133 (DRCR) | 693 subjects 840 eyes (21% bilateral) |
Change in visual acuity score from baseline at 2 years | Continuous | No | Yes | Repeated measures analysis of variance | GEE |
| NCT00320593 (COMET2) | 118 subjects 236 eyes (100% bilateral) |
Change in spherical equivalent from baseline to 3 years | Continuous | Yes | No need because an average of two eyes were used | Analysis of covariance | GEE or mixed effect model if the spherical equivalent is analyzed at eye-level |
| NCT00345176 (AREDS2) |
4203 subjects 6916 eyes (65% bilateral) |
Development of advanced AMD | Time-to-event | Yes | Yes | Marginal Cox regression model | Frailty model |
| NCT00445003 (DRCR) | 691 subjects 854 eyes (24% bilateral) |
Change in visual acuity ETDRS letter score from baseline to one year | Continuous | No | Yes | GEE | Mixed effects model |
| NCT01489189 (DRCR) | 305 subjects 394 eyes (29% bilateral) |
Change in visual acuity from baseline at 2 years | Continuous | No | Yes | GEE | Mixed effects model |
| NCT02128763 (DREAM) | 535 patients 1022 eyes (91% bilateral) |
Mean change from baseline in OSDI score at 6 and 12 Months | Continuous | Yes | No need because the primary outcome (OSDI) was a person-level measure | Linear regression model | NA |
| NCT02374060 (Point) | 192 subjects 235 eyes (22% bilateral) |
The proportion of Baseline Central Subfield Thickness Observed at 8 Weeks | Continuous | Yes | Yes | Mixed-effects model | GEE |
| NCT02634333 | 322 subjects 386 eyes (20% bilateral) |
Development of proliferative diabetic retinopathy or diabetic macular edema | Time to event | No | Yes | Marginal Cox proportional hazards model | Frailty Model |
Among the 5 trials with continuous primary outcome analyzed at eye level, the inter-eye correlation was accounted for in 3 (60%) trials using generalized estimating equations, in one trial each using mixed effects model and repeated measures analysis of variance (ANOVA). Among 2 trials with time-to-event outcomes analyzed at eye level, a marginal Cox model was applied to account for the inter-eye correlation. In one trial with binary outcome analyzed at eye level, the modified Mantel-Haenszel chi-square test was used to account for the inter-eye correlation.
4. DISCUSSION
In this study, we reviewed the characteristics of trial design and statistical analysis for forty-two NEI-funded randomized ophthalmic clinical trials conducted since 2000. We found that these trials were designed with good statistical power (≥80%) using a variety of trial designs for evaluating different treatments of eye diseases. About a quarter of these trials used a two-eye design, and statistical analysis was performed properly in almost all the trials with adjustment of inter-eye correlation when data were analyzed at eyelevel.
The outcome measures from the two eyes of a participant are usually positively correlated, proper statistical analyses are necessary to account for the inter-eye correlation [10]. Previous studies found that the correlated eye data are often analyzed inappropriately by ignoring the inter-eye correlation using statistical methods that assume independence in the data [1], [9, 11,12]. Murdoch’s study reviewed 67 clinical science papers published in the British Journal of Ophthalmology in 1995 and found that 70% of 23 papers that used two-eye design did not appropriately adjust for the inter-eye correlation [12]. Similarly, Zhang et al reviewed 56 clinical science papers published in the British Journal of Ophthalmology in 2017 and found that 85% of 39 papers that used two-eye design did not adjust for the inter-eye correlation [11]. Lee et al. reviewed 69 papers from randomized clinical trials published in the four ophthalmology journals in 2009, including Ophthalmology, JAMA Ophthalmology, American Journal of Ophthalmology, and the British Journal of Ophthalmology, and found that 62% of trials of two-eye design did not adjust for the inter-eye correlation [1]. In a recent review of 96 ophthalmic clinical trial papers published in these 4 major ophthalmology journals in 2021, Dong et al found that among 31 trials with two-eye design, 18 (58%) trials did not adjust for the inter-eye correlation [9]. Compared to the high percent of inappropriate statistical analyses of two-eye data in previous studies, the statistical analyses of two-eye data in NEI-funded trials were outstanding in that almost all the trials used two-eye design properly adjusted for the inter-eye correlation when data were analyzed at eye level. The better statistical analysis practice in the NEI-funded trials may be due to the rigorous scientific review process by the expert panel before trials were funded, the rich clinical trial experience among the investigators of the NEI-funded trials, and the support from the data coordinating center who had experience in the design and statistical analyses of similar ophthalmic trials. For the ophthalmic trials that are not funded by NEI, the more stringent oversight of the trial protocol by experienced investigators, and biostatistical consultation of experts for the proper clinical trial design and statistical analyses may improve the practice in ophthalmic trials.
Many eye diseases are bilateral, providing a unique opportunity to enroll both eyes of a participant into a trial. Our review found that about one-quarter of the NEI-funded trials used a two-eye design with less than half of them assigning two eyes to different treatment groups. Although it is advantageous to enroll both eligible eyes into a trial from a statistical perspective, many other factors have to be considered in deciding between one-eye design or two-eye design, and whether assigning two eyes in the same treatment group or different treatment group if two-eye design is used [6,13]. Enrolling both eyes in a trial sometimes can logistically complicate the process of enrollment, treatment, and follow-up, potentially introducing bias in outcome assessment. Ethically, it is sometimes challenging to enroll both eyes into a trial at the same time. In two-eye designs, two eyes assigned to the same treatment group should be considered when there are person-level outcome measures (e.g., quality of life), there is a possibility of cross-over effects in the treatment, or if systemic safety of the treatment is of interest.
This review found that more than half of the trials had continuous primary outcome measures, about a quarter of trials had binary primary outcome and over 10% of trials had time-to-event as a primary outcome. The statistical method for analyzing primary outcome data is dependent on the type of data. For independent outcome data, the analysis of variance or analysis of covariance is commonly used to evaluate the treatment effect for continuous outcome data, the Chi-square test or logistic regression model is used for categorical outcome data, and the Kaplan-Meier analysis and Cox proportional hazards model are used for time-to-event outcome data. When the outcome measures were obtained from both eyes of a participant and data were analyzed at eye level, the inter-eye correlation needed to be accounted for by using a mixed effect model or generalized estimating equations for a continuous outcome, [14] generalized estimating equations for binary outcome [15] and marginal Cox regression model for time-to-event outcome [16]. In these NEI-funded trials, appropriate methods were applied in analyzing different types of correlated two-eye data from trial participants.
In this review, we found that about one-third of the trials had more than two treatment arms which led to multiple pairwise comparisons for evaluating the efficacy of various treatments. It is well-known that multiple comparisons can lead to inflation of type I error rates (i.e., mistakenly claiming that treatment is efficacious when in truth it is not) [17]. Appropriate statistical comparisons are required to account for the multiple comparisons, so that the overall 5% type I error rate is maintained [17,18]. In this review, we found 12 (92%) out of 13 NEI-funded trials properly corrected for multiplicity by comparing multiple arms using the Bonferroni method, Hochberg procedure, or Tukey’s method. This finding suggests that the guidelines on the good practice of clinical trials are closely followed in NEI-funded trials.
Conducting a clinical trial requires a huge investment in time and resources, and failure of identification of effective treatment due to an underpowered clinical trial should be prevented. Late-phase trials are often designed with high statistical power to avoid missing the detection of clinically important treatment differences. Except for one pilot trial without providing statistical power, all the NEI-funded trials were designed with at least 80% power, with more than half of the trials having at least 90% power. However, in spite that the inter-eye correlation was accounted for in the statistical analysis, none of these trials explicitly stated in the primary result paper that the inter-eye correlation was accounted for in the sample size and statistical power calculation, although adjustment for inter-eye correlation could have been made in the trial design. Similar to our findings, Lee’s review of 69 randomized clinical trials published in 4 major clinical ophthalmology journals in 2009 also found none of these trials adjusted for the inter-eye correlation in the sample size calculation [1]. The ignorance of inter-eye correlation in sample size and power calculation could be due to a lack of procedure/software for easy adjustment of the inter-eye correlation, or due to the lack of information on the magnitude of inter-eye correlation that is needed for the precise sample size calculation for the trials with two-eye design. Lack of consideration of the inter-eye correlation could lead to over-estimation or under-estimation of the sample size and statistical power, depending on whether two eyes are assigned to the same treatment group or different treatment groups. Future collaborations are needed, including evaluating the inter-eye correlation of ocular conditions or measures and developing reporting standards to improve the practice of sample size/power calculation for the ophthalmic trials involving two eyes.
CONCLUSION
This review found that NEI-funded trials followed good practice in trial design and statistical analysis. While the availability of two eyes of a participant may complicate the trial design and statistical analysis, these NEI-funded trials were designed with adequate statistical power, took advantage of including two eyes when appropriate in the design, and properly adjusted for the inter-eye correlation in the statistical analysis. However, these trials have either not explicitly considered or reported the adjustment for the inter-eye correlation in the sample size and power calculation. Future research and education on the appropriate sample size and power calculation that accounts for the inter-eye correlation are needed to improve the design and reporting of ophthalmic trials.
AUTHORS' CONTRIBUTIONS
WZ and RZ contributed equally to the design and conduct of the study, data collection, and management, descriptive statistical analysis, as well as results interpretation and wrote the whole paper.
GSY supervised WZ and RZ for the work, adjudicated the differences in data collected by WZ and RZ, provided guidance on the design and conduct of the study, and critically reviewed, revised, and approved the manuscript.
All authors have read and approved the manuscript.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
Not applicable.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIAL
The datasets used and/or analyzed during the current study are available https://drive.google.com/drive/folders/1z_ chSveejaBHXSBIdb-C70PWCHO-rh04?usp=sharing.
FUNDING
Dr. Ying is supported by the National Eye Institute Vision Core Grant P30 EY01583.
CONFLICT OF INTEREST
The authors declare no conflict of interest financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


